0%

最小生成树

发表于 更新于 分类于 ，

前言

设G=(V,E)是一个无向连通图，求再G的所有生成树中，代价最小的生成树。

算法思路

  1. 输入：一个加权连通图，其中顶点集合为V，边集合为E；
  2. 初始化：Vnew = {x}，其中x为集合V中的任一节点（起始点），Enew = {},为空；
  3. 重复下列操作，直到Vnew = V：
    1. 在集合E中选取权值最小的边****，其中u为集合Vnew中的元素，而v不在Vnew集合当中，并且v∈V（如果存在有多条满足前述条件即具有相同权值的边，则可任意选取其中之一）；
    2. 将v加入集合Vnew中，将****边加入集合Enew中；
  4. 输出：使用集合Vnew和Enew来描述所得到的最小生成树。

源代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
#include<stdio.h>
#define n 6

typedef struct
{
    int fromvex,endvex;
    int length;
} edge;

int dist[n][n];
edge T[n-1];

void input()
{
    int i,j;
    for(i=1;i<=n;i++)
        for(j=1;j<=n;j++)
        {
            scanf("%d",&dist[i-1][j-1]);
        }
}


void PRIM()
{
    int j,k,m,v,min,max=10000;
    int d;
    edge e;
    for(j=1;j<n;j++)
    {
        T[j-1].fromvex=1;
        T[j-1].endvex=j+1;
        T[j-1].length=dist[0][j];
    }
    for(k=0;k<n-1;k++)
    {
        min=max;
        for(j=k;j<n-1;j++)
        {
            if(T[j].length<min)
            {
                min=T[j].length;
                m=j;
            }
        }
        e=T[m];T[m]=T[k];T[k]=e;
        v=T[k].endvex;
        printf("The %d edge: %d---%d ,cost: %d\n",k+1,T[k].fromvex,T[k].endvex,T[k].length);
        for(j=k+1;j<n-1;j++)
        {
            d=dist[v-1][T[j].endvex-1];
            if(d<T[j].length)
            {
                T[j].length=d;
                T[j].fromvex=v;
            }
        }
    }
}

int main()
{
    input();
    PRIM();
    return 0;
}
/*
 * 测试数据
8 6 1 5 8 8
6 8 5 8 3 8
1 5 8 7 5 4
5 8 7 8 8 2
8 3 5 8 8 6
8 8 4 2 6 8
 */

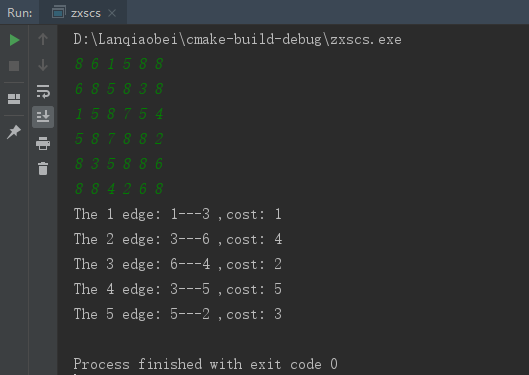
运行结果

1