方格填数 | 执念の博客

前言

方格填数（回溯算法求解）

回溯算法实际上一个类似枚举的搜索尝试过程，主要是在搜索尝试过程中寻找问题的解，当发现已不满足求解条件时，就“回溯”返回，尝试别的路径。回溯法是一种选优搜索法，按选优条件向前搜索，以达到目标。但当探索到某一步时，发现原先选择并不优或达不到目标，就退回一步重新选择，这种走不通就退回再走的技术为回溯法，而满足回溯条件的某个状态的点称为“回溯点”。许多复杂的，规模较大的问题都可以使用回溯法，有“通用解题方法”的美称。
回溯法有通用解法的美称，对于很多问题，如迷宫等都有很好的效果。回溯算法实际上一个类似枚举的深度优先搜索尝试过程，主要是在搜索尝试过程中寻找问题的解，当发现已不满足求解条件时，就“回溯”返回（也就是递归返回），尝试别的路径。许多复杂的，规模较大的问题都可以使用回溯法，有“通用解题方法”的美称。回溯法说白了就是穷举法。回溯法一般用递归来解决。

回溯

回溯法一般都用在要给出多个可以实现最终条件的解的最终形式。回溯法要求对解要添加一些约束条件。总的来说，如果要解决一个回溯法的问题，通常要确定三个元素：

选择。对于每个特定的解，肯定是由一步步构建而来的，而每一步怎么构建，肯定都是有限个选择，要怎么选择，这个要知道；同时，在编程时候要定下，优先或合法的每一步选择的顺序，一般是通过多个if或者for循环来排列。
条件。对于每个特定的解的某一步，他必然要符合某个解要求符合的条件，如果不符合条件，就要回溯，其实回溯也就是递归调用的返回。
结束。当到达一个特定结束条件时候，就认为这个一步步构建的解是符合要求的解了。把解存下来或者打印出来。对于这一步来说，有时候也可以另外写一个issolution函数来进行判断。注意，当到达第三步后，有时候还需要构建一个数据结构，把符合要求的解存起来，便于当得到所有解后，把解空间输出来。这个数据结构必须是全局的，作为参数之一传递给递归函数。

对于回溯法来说，每次递归调用，很重要的一点是把每次递归的不同信息传递给递归调用的函数。而这里最重要的要传递给递归调用函数的信息，就是把上一步做过的某些事情的这个选择排除，避免重复和无限递归。另外还有一个信息必须传递给递归函数，就是进行了每一步选择后，暂时还没构成完整的解，这个时候前面所有选择的汇总也要传递进去。而且一般情况下，都是能从传递给递归函数的参数处，得到结束条件的。
递归函数的参数的选择，要遵循四个原则：

必须要有一个临时变量(可以就直接传递一个字面量或者常量进去)传递不完整的解，因为每一步选择后，暂时还没构成完整的解，这个时候这个选择的不完整解，也要想办法传递给递归函数。也就是，把每次递归的不同情况传递给递归调用的函数。
可以有一个全局变量，用来存储完整的每个解，一般是个集合容器（也不一定要有这样一个变量，因为每次符合结束条件，不完整解就是完整解了，直接打印即可）。
最重要的一点，一定要在参数设计中，可以得到结束条件。一个选择是可以传递一个量n，也许是数组的长度，也许是数量，等等。
要保证递归函数返回后，状态可以恢复到递归前，以此达到真正回溯。

题目

如下的10个格子
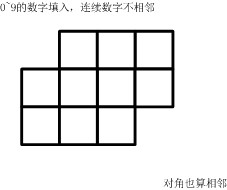
填入0~9的数字。要求：连续的两个数字不能相邻。
（左右、上下、对角都算相邻）
一共有多少种可能的填数方案？
请填写表示方案数目的整数。
注意：你提交的应该是一个整数，不要填写任何多余的内容或说明性文字。

算法思路

首先我想到的就是回溯，比如第一个格子从0-9抓一个，然后第二个格子只能从剩下里面抓，并且每填写一个格子，就判断可以继续么（即满足连续的两个数字不能相邻么），然后如果OK，那么继续，直到最后一个格子能填上，就把次情况记录下来，但是如果判断不行，那么回溯上一个，继续遍历下一个可以抓的的数字，直到遍历完为止。

算法的伪代码：（将此框框补满补成五行六列的二维数组，是为了防止遍历判断的时候下标越界）

输入：无

输出：有多少种可能的填数方案

定义一个a[5][6]五行六列的二维数组。
定义一个vis[10]有十个元素的一维数组用来标记是否被访问过。
定义一个ans计数器。
初始化数组(数组全部赋值为-10)
传入(1,2)给f函数。
1. f函数：if (x == 3 && y == 4)//即到达最末尾的格子
  1. 计数器ans++
  2. 否则for (int i = 0; i < 10; ++i)//从0-9抓一个
    1. if (vis[i] == 0) //i没有被用过
      1. a[x][y] = i //填入数字
      2. if(!check(x,y))//判断是否合法（即是否能满足连续的两个数字不能相邻么，check函数的思路最后再写了\）
        
        若不合法，a[x][y]=-10 //把-10恢复并跳出此循环continue
        
        否则 vis[i] = 1 //标记为已访问
        
        if (y == 4)//如果y到4了，换行
        
        f(x + 1, 1)//传入换行后的位置
        
        否则，f(x, y + 1)//传入下一个位置
        
        vis[i] = 0 a[x][y]=-10//将此标记恢复，并且将此位置的值恢复为-10
输出计数器ans的值。

check**函数的伪代码：**

遍历穿入位置的i，j为a[i][j]此位置的附近包括自己9个格子的数字为a[x][y]
1. 判断,如果a[x][y] - a[i][j]的绝对值为1（说明两数相邻）
  1. 返回False
遍历完毕也没有返回False，说明检查通过，返回True

源代码

//
// Created by ZhiNian on 2019/4/29.
//

#include <iostream>
#include <cmath>

using namespace std;

int a[5][6];//记录每个位置的值
int vis[10];//记录0-9是否被用过
int ans;//记录下每一次可行的填数

bool check(int i, int j) {//检查
    for (int x = i - 1; x <= i + 1; ++x) {//横向的此位置的左边一个到右边一个
        for (int y = j - 1; y <= j + 1; ++y) {//纵向的的此位置上面一个到下面一个
            if (abs(a[x][y] - a[i][j]) == 1)//如果与原数差的绝对值为1 ，说明相邻
                return false;//返回False
        }
    }
    return true;//遍历完都没有返回，那么说明符合，返回True
}

void f(int x, int y) {
    if (x == 3 && y == 4) {//遍历到了最后一个位置
        ans++;//此填数方法可行，则计数器加一
        return;//返回函数，因为为void函数，所以返回无
    }

    for (int i = 0; i < 10; ++i) {//从0~9中抓一个
        if (vis[i] == 0) {//检查是否使用过
            a[x][y] = i;//填数
            if (!check(x, y)) {//不合法
                a[x][y] = -10;//恢复-10
                continue;//跳出循环继续
            }
            vis[i] = 1;//若合法，标记为已访问
            if (y == 4)//如果到第四列了
                f(x + 1, 1);//传入换行的位置给f递归
            else//否则
                f(x, y + 1);//传入下一个的位置给f递归

            vis[i] = 0;//回溯恢复标记为0
            a[x][y] = -10;//回溯恢复值为-10
        }
    }

}

void init() {
    for (int i = 0; i < 5; ++i) {//从第1行到第5行
        for (int j = 0; j < 6; ++j) {//从第1列到第6列
            a[i][j] = -10;//全部赋值为-10
        }
    }
}

int main(int argc, const char *argv[]) {
    init();//初始化二维数组
    f(1, 2);//传入入口位置
    cout << ans << endl;//输出计数器的值
    return 0;
}

运行结果

时间复杂度

空间复杂度

总结

这一次的试验内容很具有代表性，通过上机操作实践与对问题的思考，让我更深层次领悟了回溯法的思想。
回溯算的基本思路并不难理解，简单来说就是：从一条路往前走，能进则进，不能进则退回来，换另一条路再试试。回溯法的基本做法是深度优先搜索，是一种组织得仅仅有条的、能避免不必要重复的穷举式搜索算法。